双边滤波与快速双边滤波
Bilateral filter
Bilateral filter
https://blog.csdn.net/DDDDWJDDDD/article/details/146882642
https://people.csail.mit.edu/sparis/publi/2006/eccv/Paris_06_Fast_Approximation.pdf
The bilateral filter was first introduced by Smith and Brady under the name “SUSAN” .It was rediscovered later by Tomasi and Manduchi [1] who called it the “bilateral filter” which is now the most commonly used name.
空间权重 + 颜色权重
双边滤波的计算依赖两个权重:
空间权重(几何权重)spatial domain S :基于像素之间的物理距离,决定了相邻像素的影响程度,通常使用高斯函数计算: \[ f_d(\|x-y\|)=e^{-\frac{\|x-y\|^2}{2 \sigma_s^2} } \]
- 由参数 sigmaSpace 控制,值越大,远处的像素影响越大。
- 作用类似于高斯模糊,限制远距离像素的影响。
颜色权重(强度权重)the range domain R:基于像素灰度值(或颜色)之间的相似性,决定了颜色接近的像素影响程度,通常使用高斯函数计算: \[ f_r(|I(x)-I(y)|)=e^{-\frac{|I(x)-I(y)|^2}{2 \sigma_r^2} } \]
- 颜色相近的像素权重较高,差异较大的像素影响较小,从而防止边缘模糊。
- 由参数 sigmaColor 控制,值越大,即使颜色相差较大仍然会被平滑。
最终的权重由两者的乘积决定: \[ w(x, y)=f_d(\|x-y\|) \cdot f_r(|I(x)-I(y)|) \]
\[ w(i, j, k, l)=w_d(i, j, k, l) * w_r(i, j, k, l)=\exp \left(-\frac{(i-k)^2+(j-l)^2}{2 \sigma_d^2}-\frac{\|f(i, j)-f(k, l)\|^2}{2 \sigma_r^2}\right) \]
因此,双边滤波器的数据公式可以表示如下: \[ g(i, j)=\frac{\left.\left.\sum_{k l} f(k, l) w(i, j, k, l)\right)\right)}{\sum_{k l} w(i, j, k, l)} \]
代码实现
略,有很多,但速度慢
- 空域sigma(space选取:
sigma(space)越大,图像越平滑,趋于无穷大时,每个权重都一样,类似均值滤波。
sigma(space)越小,中心点权重越大,周围点权重越小,对图像的滤波作用越小,趋于零时,输出等同于原图。
- 值域sigma(color选取:
Sigma(color)越大,边缘越模糊,极限情况为simga无穷大,值域系数近似相等(忽略常数时,将近为exp(0)= 1),与高斯模板(空间域模板)相乘后可认为等效于高斯滤波。
Sigma(color)越小,边缘越清晰,极限情况为simga无限接近0,值域系数除了中心位置,其他近似为0(接近exp(-∞) =0),与高斯模板(空间域模板)相乘进行滤波的结果等效于源图像。
- 邻域直径d:
小值(如 5):影响范围小,平滑效果较弱,但边缘保持较好。
大值(如 15+):影响范围大,平滑更强,但可能损失更多细节
空间域sigma选取:其中核大小通常为sigma的6*sigma + 1。因为离中心点3*sigma大小之外的系数与中点的系数只比非常小,可以认为此之外的点与中心点没有任何联系
fast bilateral filter
REF:
https://people.csail.mit.edu/sparis/publi/2006/eccv/Paris_06_Fast_Approximation.pdf
https://zhuanlan.zhihu.com/p/272236618
动机
由于 bilateral filter 的 空间kernel是固定的, 但是 和周围像素点的灰度值差kernel却是要每个像素实时计算的,因此在计算过程中,不能用卷积,导致计算时间很长.
我们知道空域的kernel是根据周围像素点相对于当前像素点的偏移量进行的,那么能否加上把像素值也纳入坐标系, 这样远离的像素值就像是远离的坐标,拥有更低的权重,这样就形成了 x,y,value的 表征空间和卷积核.这样图像就可以用卷积加快计算了, fast bilateral filter 就是利用了这个思想.
卷积: \[ I_p=\sum _{q\in \mathcal{K} } kernel(\|\mathbf{p}-\mathbf{q}\|)*I_q \]
\[ \circledast \]
二维的卷积数值化表示:
\[Y(i,j)=\sum_{m=0}^{k_{h}-1}\sum_{n=0}^{k_{w}-1}X(i+m,j+n)\cdot K(m,n)\]
三维的卷积数值化表示
\[Y(d,i,j)=\sum_{p=0}^{k_{d}-1}\sum_{m=0}^{k_{h}-1}\sum_{n=0}^{k_{w}-1}X(d+p,i+m,j+n)\cdot K(p,m,n)\]
bilateral filter 转为卷积
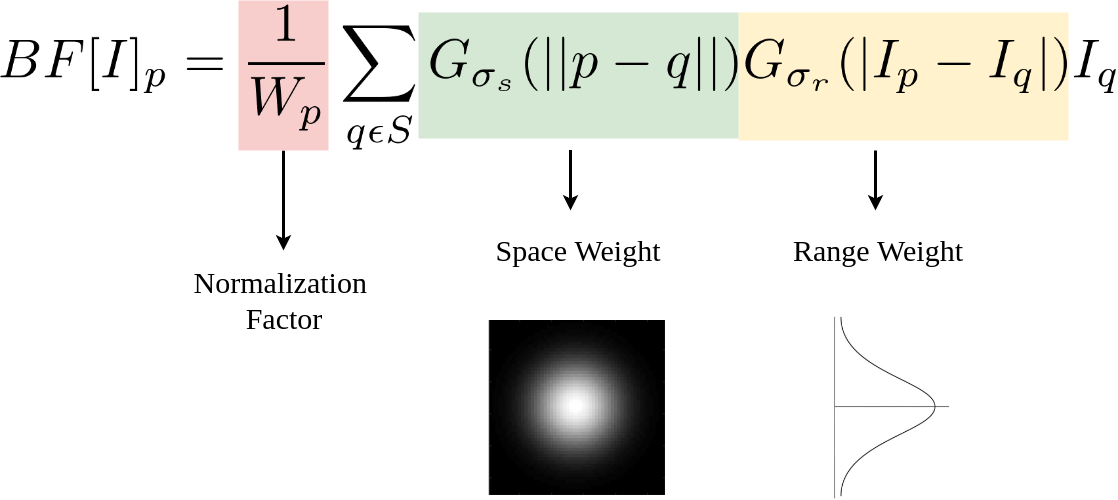
为了核论文保持一致,我们将上面bilater filter 公式换一种表示: \[ \begin{aligned} I_{\mathbf{p} }^{\mathrm{bf} } & =\frac{1}{W_{\mathbf{p} }^{\mathrm{bf} }} \sum_{\mathbf{q} \in \mathcal{S} } G_{\sigma_{\mathrm{s} }}(\|\mathbf{p}-\mathbf{q}\|) G_{\sigma_{\mathrm{r} }}\left(\left|I_{\mathbf{p} }-I_{\mathbf{q} }\right|\right) I_{\mathbf{q} } \\ \text { with } \quad W_{\mathbf{p} }^{\mathrm{bf} } & =\sum_{\mathbf{q} \in \mathcal{S} } G_{\sigma_{\mathrm{s} }}(\|\mathbf{p}-\mathbf{q}\|) G_{\sigma_{\mathrm{r} }}\left(\left|I_{\mathbf{p} }-I_{\mathbf{q} }\right|\right) \end{aligned} \] 可以看到\(I_{\mathbf{p} }^{\mathrm{bf} }\)和\(\quad W_{\mathbf{p} }^{\mathrm{bf} }\)两个公式有相同的部分,用向量形式更凸显共同部分: 值(Iq,1)构成一个列向量
\[ \left(W_{\mathbf{p}}^{\mathrm{bf}},\ I_{\mathbf{p}}^{\mathrm{bf}}\right) = \sum_{\mathbf{q} \in \mathcal{S}} G_{\sigma_{\mathrm{s}}}\!\bigl(\|\mathbf{p} - \mathbf{q}\|\bigr) G_{\sigma_{\mathrm{r}}}\!\bigl(|I_{\mathbf{p}} - I_{\mathbf{q}}|\bigr) \begin{pmatrix} I_{\mathbf{q}} \\[4pt] 1 \end{pmatrix} \]
这里的1可以用Wq=1来代替,得到
\[ \left(W_{\mathbf{p}}^{\mathrm{bf}},\ I_{\mathbf{p}}^{\mathrm{bf}}\right) = \sum_{\mathbf{q}\in S} G_{\sigma_{\mathrm{s}}}\!\bigl(\|\mathbf{p}-\mathbf{q}\|\bigr)\, G_{\sigma_{\mathrm{r}}}\!\bigl(|I_{\mathbf{p}}-I_{\mathbf{q}}|\bigr)\, \begin{pmatrix} W_{\mathbf{q}} I_{\mathbf{q}} \\[4pt] W_{\mathbf{q}} \end{pmatrix} \]
但由于前面的weiget 依赖于 \(G_{\sigma_{\mathbf{q} }}(|I_{\mathbf{p} }-I_{\mathbf{q} }|)\) ,不是固定的,
于是文章新增了一个表示灰度值的维度\(\zeta\), 它的定义域是图片像素点数值的定义域.
并引入 Kronecker 函数. 根据 Kronecker symbol δ(ζ) (1 if ζ = 0, 0 otherwise) 定义, 可知:\[\left[\delta(\zeta-I_{\mathbf{q} })=1\right]\Leftrightarrow\left[\zeta=I_{\mathbf{q} }\right]\], 于是可以重写为:
\[ \begin{pmatrix} W_{\mathbf{p}}^{\mathrm{bf}} I_{\mathbf{p}}^{\mathrm{bf}} \\[6pt] W_{\mathbf{p}}^{\mathrm{bf}} \end{pmatrix} = \sum_{\mathbf{q}\in\mathcal{S}} \sum_{\zeta\in\mathcal{R}} G_{\alpha_{\mathbf{q}}}\!\bigl(\|\mathbf{p}-\mathbf{q}\|\bigr)\, G_{\alpha_{\mathbf{q}}}\!\bigl(|I_{\mathbf{p}}-\zeta|\bigr)\, \delta(\zeta - I_{\mathbf{q}}) \begin{pmatrix} W_{\mathbf{q}} I_{\mathbf{q}} \\[6pt] W_{\mathbf{q}} \end{pmatrix} \]
接下来 我们要把原先二维的weight(或者说kernel)转为三维的kernel.,把后面的表示xy二维空间的列向量,转为三维空间的列向量.
- 二维转三维卷积kernel
首先,\({\mathrm{S} }\times{\mathrm{R} }\) 积空间(product space) 已经是一个 三维空间: x,y, grayvalue
其次,\(\sum_{\mathbf{q}\in{\mathcal{S} }}\sum_{\zeta\in{\mathcal{R} }}=\sum_{(\mathbf{q},\zeta)\in{\mathcal{S} }\times{\mathcal{R} }}\) ,是三个变量的积分
于是定义 \[ G_{\sigma}\!\bigl(\mathbf{p}, \mathbf{q}, \zeta \bigr) = G_{\sigma_{\mathrm{s}}}\!\bigl(\|\mathbf{p}-\mathbf{q}\|\bigr)\, G_{\sigma_{\mathrm{r}}}\!\bigl(|I_{\mathbf{p}}-\zeta|\bigr) \] 作为 高斯kernel
那么卷积核就构造完成
- 构造被卷积三维图像
首先,将\(\delta(\zeta-I_{\mathbf{q} })\) 移到后面的列向量里 \[ \left(\begin{array}{l}{\delta(\zeta-I_{\mathbf{q} }){W_{\mathbf{q} }\ I_{\mathbf{q} }} }\\ {\delta(\zeta-I_{\mathbf{q} }){W_{\mathbf{q} }} }\end{array}\right) \] 我们构造两个函数 \(i\; and\; w\) \[ \begin{aligned} w(q,\zeta) &:\; (\mathbf{q}\in\mathcal{S},\ \zeta\in\mathcal{R}) \;\mapsto\; \delta(\zeta - I_{\mathbf{q}})\,W_{\mathbf{q}}, \\[6pt] i(q,\zeta) &:\; (\mathbf{q}\in\mathcal{S},\ \zeta\in\mathcal{R}) \;\mapsto\; w(q,\zeta)\,I_{\mathbf{q}}. \end{aligned} \]
那么列向量可以变换为: \[ \begin{pmatrix} w(\mathbf{q},\zeta)\,i(\mathbf{q},\zeta) \\[6pt] w(\mathbf{q},\zeta) \end{pmatrix} \]
基于Kronecker 函数, 这两个函数具有以下关系:
- 当且仅当 \(\zeta = I_q\),时 \(w(q,\zeta)=W_q=1\)
- 于是自然而然, 当且仅当 \(\zeta = I_q\),时 \(i(q,\zeta)=I_q\)
从 x,y,ζ 坐标的图像上来看
列向量的第一个元素,对应的图像\(A\) 是 W*H*Depth尺寸, 在 \(\zeta = I(x,y)\) 时候, \(A(x,y,\zeta) = I(x,y)\)
列向量的第二个元素,对应的图像\(B\) 是 W*H*Depth尺寸, 在 \(\zeta = I(x,y)\) 时候, \(B(x,y,\zeta) = 1\)
这样被卷积三维图像 就构造好了,变换的过程大致这样

这样就完成了到三维空间的卷积
于是通过卷积,我们得到了 分子和分母,相除就是滤波后的图片 \[ \begin{aligned} \bigl(w^{\mathrm{bf}} i^{\mathrm{bf}},\ w^{\mathrm{bf}}\bigr) &= g_{\sigma_{\mathrm{s}},\sigma_{\mathrm{r}}} \otimes (w i,\ w), \\[8pt] I_{\mathbf{p}}^{\mathrm{bf}} &= \frac{w^{\mathrm{bf}}(\mathbf{p}, I_{\mathbf{p}})\ i^{\mathrm{bf}}(\mathbf{p}, I_{\mathbf{p}})} {w^{\mathrm{bf}}(\mathbf{p}, I_{\mathbf{p}})}. \end{aligned} \]
代码实现
为了加快运算, 又考虑到图像是做模糊操作,于是文章里又做了一部降采样进行处理
这里以OzgurBagci实现的fastbilater为对象分析
1 | def bilateral(image, sigmaspatial, sigmarange, samplespatial=None, samplerange=None): |
- 假设原本传入的变量为: 空间 sigmaspatial=7, 数值 sigmarange=22,图片使用 空间降采样samplespatial =3, 数值降采样 samplerange=9
- 那么对到降采样后的各个变量新的数值
sigma
- 空间 derivedspatial = sigmaspatial / samplespatial =2.3
- 数值 derivedrange = sigmarange / samplerange =2.4
kernel的大小空间和数值分别设置为2倍sigma和4倍sigma,因此
空间kernel直径 int(derivedspatial * 2 + 1) =5
数值kernel直径 int(2 * derivedrange * 2 + 1=10
padding 大小: (其实这里不用padding,因为后面的convolve由于设置了mode 自动pad了,)
- 空间 xypadding = round(2 * derivedspatial + 1)
- 数值 zpadding = round(2 * derivedrange + 1)
降采样后的图片大小:
- samplewidth = int(round((width - 1) / samplespatial) + 1 + 2 * xypadding)
- sampleheight = int(round((height - 1) / samplespatial) + 1 + 2 * xypadding)
- sampledepth = int(round(edgedelta / samplerange) + 1 + 2 * zpadding)
构造三维图像:
创建空的samplewidth * sampleheight * sampledepth 数组 ,表示降采样后(x,y,value-minvalue) 的灰度值value, 减去minvalue是为了节省不必要的空间,因为没有这个值
- dataflat = np.zeros(sampleheight * samplewidth * sampledepth)
生成图像的索引坐标
- (ygrid, xgrid) = np.meshgrid(range(width), range(height))
- dimx = np.around(xgrid / samplespatial) + xypadding
- dimy = np.around(ygrid / samplespatial) + xypadding
生成图像的深度索引坐标
- dimz = np.around((image - edgemin) / samplerange) + zpadding
接下来要把原图像的数值填进创建的三维空图像dataflat
- dimx,dimy,dimz 先flatten: flatx,flaty,flatz
- dataflat[flatz + flaty * sampledepth + flatx * samplewidth * sampledepth] = flatimage ,这时候 dataflat的size 多数情况下是比 flatimage 大很多的,因为它有很多空白值.
但要注意,由于降采样的缘故, 原图中相邻位置和,相近亮度的点会落到同一个dataflat 的索引位置:
比如原图共942000 像素点, 但是到index(=flatz + flaty * sampledepth + flatx * samplewidth * sampledepth), 它的集合大小为678717,少了1/4,说明有1/4的点发生了后面覆盖前面出现
举例来说原图像:
X=256 Y=1127 Gray=66.86253 X=256 Y=1128 Gray=68.36141 X=257 Y=1128 Gray=67.08282
降采样后落到的坐标
X=134.0 Y=570.0 Z=20.0 X=134.0 Y=570.0 Z=20.0 X=134.0 Y=570.0 Z=20.0
最后这个坐标幅值为:67.08282
但数值接近,影响不大
dataflat 重新reshape为 (sampleheight, samplewidth, sampledepth), 命名data
拷贝一份data,作为后面要计算的weights,类型为bool
卷积核:
1
2
3
4
5
6
7
8
9
10
11
12kerneldim = derivedspatial * 2 + 1
kerneldep = 2 * derivedrange * 2 + 1
halfkerneldim = round(kerneldim / 2)
halfkerneldep = round(kerneldep / 2)
(gridx, gridy, gridz) = np.meshgrid(range(int(kerneldim)), range(int(kerneldim)), range(int(kerneldep)))
gridx -= int(halfkerneldim)
gridy -= int(halfkerneldim)
gridz -= int(halfkerneldep)
gridsqr = ((gridx * gridx + gridy * gridy) / (derivedspatial * derivedspatial)) +((gridz * gridz) / (derivedrange * derivedrange))
kernel = np.exp(-0.5 * gridsqr)插值回原尺寸
- 重新创建浮点坐标
1
2
3dimx = (xgrid / samplespatial) + xypadding
dimy = (ygrid / samplespatial) + xypadding
dimz = (image - edgemin) / samplerange + zpadding- 插值
1
2interpolate.interpn((range(normalblurdata.shape[0]), range(normalblurdata.shape[1]),
range(normalblurdata.shape[2])), normalblurdata, (dimx, dimy, dimz))- 插值出来的尺寸和dimx 保持一致,就是原图尺寸
再次讨论各个size的作用
dimz1 = np.around((image - edgemin) / samplerange) + zpadding
sampledepth = int(round(edgedelta / samplerange) + 1 + 2 * zpadding)
dimz2 = (image - edgemin) / samplerange + zpadding
第一个dzim是给降维后的data空图索引赋值用的,第二个是data图的第三维sampledepth 的大小,第三个是最后插值回原尺寸用的浮点坐标
假设zpadding=0, zdim是四舍五入,sampledepth 是向下取整+1, dimz 是浮点,有可能出现
- sampledepth >= dimz2.max()>dimz1.max() >= sampledepth -1
- sampledepth >= dimz1.max()>dimz2.max() >= sampledepth -1
这样看似不会在插值的时候出现 dimz2 的值超出 sampledepth 情况,导致插值失败,但是由于sampledepth 是用于创建第三维度大小sampledepth ,实际的取值范围是 [0,sampledepth-1],所以是很容易越界报错的
所以源代码可以做如下修改
- 去除xypadding和zpadding, 因为没有用
- sampledepth 最好修改为 : sampledepth = int(round(edgedelta / samplerange) + 2 ), 另外两个维度同理
导向滤波*
#TODO
